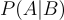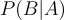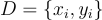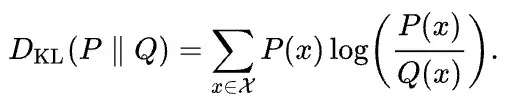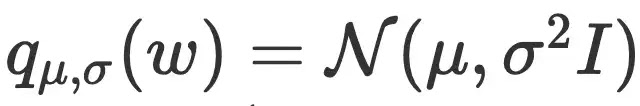Dari Teori Ke Praktek dengan Bayesian Neural Network, Menggunakan Python

Fisika dan teknik adalah dua ilmu berbeda yang sama-sama ingin memahami alam dan kemampuan untuk memodelkannya.

Pendekatan fisikawan lebih teoretis. Fisikawan melihat dunia dan coba memodelkannya dengan seakurat mungkin. Realita yang dimodelkan fisikawan tidak sempurna dan mempunyai prediksi, tapi demikian kita memperhitungkan tidak sempurnanya ini, realita jadi rapi, sempurna, dan menawan.

Pendekatan seorang insinyur jauh lebih praktis. Insinyur menyadari semua batasan model fisikawan dan mencoba membuat pengalaman di laboratorium semulus mungkin. Insinyur mungkin melakukan perkiraan yang lebih brutal (misalnya pi = 3) tetapi perkiraannya sebenarnya lebih efisien dalam eksperimen kehidupan nyata.

Perbedaan antara pendekatan praktis seorang insinyur dan pendekatan elegan dan teoretis seorang fisikawan diringkas oleh kutipan dari Gordon Lindsay Glegg ini:

Seorang ilmuwan dapat menemukan bintang baru, tetapi ia tidak dapat membuatnya. Dia harus meminta seorang insinyur untuk melakukannya untuknya.

Dalam kehidupan sehari-hari seorang peneliti, cara kerjanya seperti ini. Seorang fisikawan adalah seseorang yang memiliki teori tentang fenomena tertentu. Seorang insinyur adalah seorang ilmuwan yang dapat mengatur percobaan dan melihat apakah teorinya berhasil.

Sekarang secara praktis, ketika saya memulai transisi ini dari fisikawan menjadi insinyur, salah satu pertanyaan yang sering saya tanyakan adalah sebagai berikut:

"Oke, model Anda tampaknya berfungsi... tetapi seberapa tangguh model itu?"

Ini adalah pertanyaan khas seorang insinyur.

Ketika Anda memiliki model fisik, dengan kondisi tertentu, model tersebut secara teoritis sempurna.

Meskipun demikian, saat Anda melakukan eksperimen, ada tingkat kesalahan tertentu, dan Anda harus dapat memperkirakannya dengan benar.

Dalam contoh khusus yang sedang kita lakukan ini, bagaimana kita memperkirakan perbedaan energi antara keluaran teoretis dan hasil percobaan

Dua pilihan:

A. Jika model bersifat deterministik, Anda dapat mengubah kondisi awal dengan delta tertentu (mis. menerapkan aturan deterministik tersebut ke versi input yang berisik)

B. Jika modelnya probabilistik, untuk beberapa input yang diberikan, Anda mengekstrak beberapa informasi statistik dari output (misalnya rata-rata, deviasi standar, batas ketidakpastian…)

Sekarang mari masuk ke bahasa pembelajaran mesin. Dalam kasus khusus ini:

A. Jika model pembelajaran mesin bersifat deterministik, kita dapat menguji kekokohannya dengan mengocok set pelatihan dan validasi.

B. Jika model pembelajaran mesin bersifat probabilistik, untuk beberapa input yang diberikan, Anda mengekstrak beberapa informasi statistik dari output (mis. rata-rata, deviasi standar, batas ketidakpastian…)

Sekarang, katakanlah model yang ingin kita gunakan adalah jaringan saraf.Pertanyaan pertama: apakah Anda memerlukan Neural Network? Jika jawabannya ya, maka Anda harus menggunakannya (Anda tidak mengatakannya). Pertanyaan:

“Apakah model pembelajaran mesin Anda tangguh?”

Definisi asli dari jaringan saraf adalah "murni deterministik." Kita dapat mengocok set pelatihan, validasi, dan pengujian, tetapi kita perlu mempertimbangkan bahwa jaringan saraf membutuhkan waktu lama untuk dilatih, dan jika kita ingin melakukan beberapa pengujian (misalkan CV = 10.000), Anda mungkin harus melakukannya Tunggu sebentar.

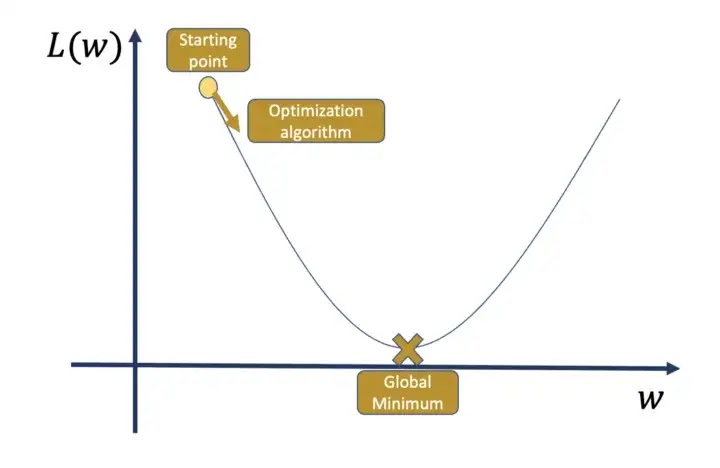
Hal lain yang perlu kita pertimbangkan adalah jaringan saraf dioptimalkan menggunakan algoritme yang dikenal sebagai gradient descent. Idenya adalah kita mulai dari titik di ruang parameter dan, seperti namanya, turun ke arah yang ditunjukkan oleh gradien negatif kerugian. Ini idealnya akan membawa kita ke minimum global (spoiler: sebenarnya tidak pernah global).

Situasi ideal untuk fungsi kerugian 1D sederhana yang tidak realistis adalah sebagai berikut:

Sekarang, dalam situasi ini, jika kita mengubah titik awal, kita masih menyatu dengan satu-satunya minimum global.

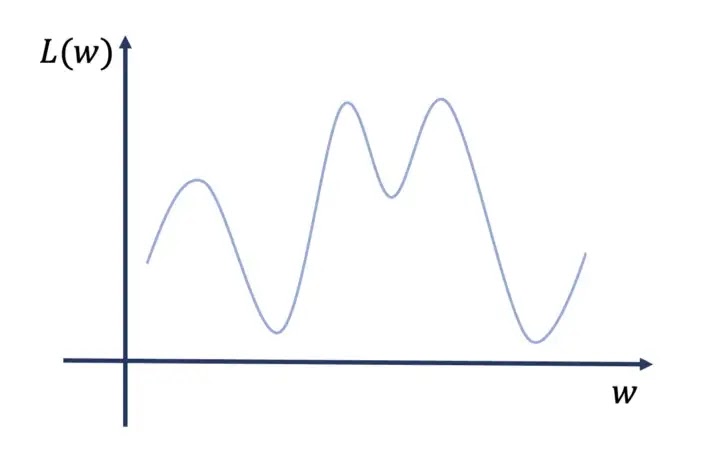
Situasi yang lebih realistis adalah seperti ini:

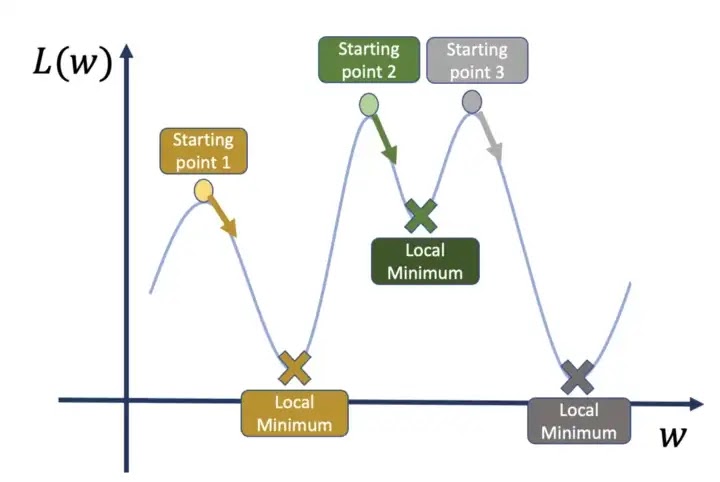
Jadi, jika kita memulai ulang algoritme pelatihan secara acak dari titik awal yang berbeda, kita menyatu ke minima lokal yang berbeda.

Jadi jika kita mulai dari titik 1 atau titik 3, kita mendapatkan titik yang lebih rendah dari titik awal 2.

Fungsi kerugian berpotensi penuh dengan minima lokal, sehingga menemukan minimum global yang sebenarnya bisa menjadi tugas yang sulit. Hal lain yang dapat kami lakukan adalah memulai kembali pelatihan dari titik awal yang berbeda dan membandingkan nilai fungsi kerugian. Kami memiliki masalah yang sama seperti sebelumnya dengan pendekatan ini: kami hanya dapat melakukannya berkali-kali.

Ada pendekatan yang lebih kuat, ketat, dan elegan untuk menggunakan kekuatan komputasi yang sama dari jaringan saraf dengan cara probabilistik; itu disebut Bayesian Neural Networks.

Pada artikel ini, kita akan belajar:

Gagasan di balik Bayesian Neural Networks

Rumusan matematis dibalik Bayesian Neural Network

Implementasi Bayesian Neural Networks menggunakan Python (lebih spesifik Pytorch)

Cara mengatasi masalah regresi menggunakan Bayesian Neural Network

Ayo mulai!

1. Apa itu Jaringan Syaraf Bayesian?

Seperti yang kami katakan sebelumnya, gagasan tentang jaringan saraf Bayesian adalah menambahkan "akal" probabilistik ke jaringan saraf biasa. Bagaimana kita melakukannya?

Sebelum memahami jaringan saraf Bayesian, kita mungkin harus meninjau sedikit teorema Bayes.

Cara yang sangat efisien untuk melihat teorema Bayes adalah sebagai berikut:

“Teorema Bayes adalah teorema matematika yang menjelaskan mengapa jika semua mobil di dunia berwarna biru maka mobil saya harus berwarna biru, tetapi hanya karena mobil saya berwarna biru tidak berarti semua mobil di dunia berwarna biru. ”

Dalam istilah matematika, mengingat peristiwa "A" dan "B", peluang terjadinya peristiwa "A" jika peristiwa "B" telah terjadi adalah sebagai berikut:

Dan peluang kejadian “B” terjadi jika kejadian “A” telah terjadi adalah sebagai berikut:

Persamaan yang menghubungkan ekspresi pertama dan terakhir adalah sebagai berikut:

Oke? Hebat. Sekarang, katakanlah Anda memiliki model jaringan saraf Anda. Jaringan saraf ini tidak lebih dari sekumpulan parameter yang mengubah input yang diberikan menjadi output yang diinginkan.

Jaringan saraf feed-forward (struktur pembelajaran mendalam yang paling sederhana) memproses input Anda dengan mengalikan input dengan matriks parameter. Kemudian fungsi aktivasi non-linear (ini adalah kekuatan sebenarnya dari jaringan saraf) diterapkan secara masuk akal ke hasil perkalian matriks ini. Hasilnya adalah masukan dari lapisan berikutnya, di mana prosedur yang sama diterapkan.

Sekarang kita akan mengacu pada set parameter model sebagai w. Sekarang kita bisa bertanya pada diri sendiri pertanyaan rumit ini.

Katakanlah saya memiliki dataset D yang merupakan kumpulan pasangan input x_i dan output y_i, misalnya, gambar hewan ke-i dan label ke-i (kucing atau anjing):

Berapa probabilitas memiliki satu set parameter, mengingat set data tertentu D?

Anda mungkin perlu membaca pertanyaan ini 3 atau 4 kali untuk memahaminya, tetapi idenya ada. Jika Anda memiliki pemetaan tertentu antara input dan output, dalam kasus deterministik ekstrem, hanya satu set parameter yang dapat memproses input dan memberikan Anda output yang diinginkan. Dengan cara probabilistik, akan ada sekumpulan parameter probabilitas yang lebih mungkin dari parameter lainnya.

Jadi yang kami minati adalah kuantitasnya.

Sekarang, tiga hal yang cukup keren tentang itu:

1. Anda masih dapat melihatnya sebagai model jaringan saraf standar jika Anda mempertimbangkan nilai rata-rata yang diberikan distribusi tersebut. Sebagai contoh:

Sedangkan sebelah kiri dari persamaan mewakili output rata-rata yang dihitung, sebelah kanan mewakili rata-rata dari semua set yang mungkin dari hasil parameter (N), dengan distribusi probabilitas memberikan bobot untuk setiap hasil.

2. Meskipun p(w|D) jelas merupakan misteri, p(D|w) adalah sesuatu yang selalu dapat kita kerjakan. Jika kita menggunakan persamaan di atas untuk N yang besar, pembelajaran mesin tidak diperlukan. Anda dapat dengan mudah mengatakan: "coba semua model yang mungkin diberikan Jaringan Neural tertentu dan timbang semua hasil yang mungkin menggunakan persamaan di atas"

3. Saat kita mendapatkan p, kita tidak hanya mendapatkan model pembelajaran mesin; kami hampir mendapatkan model pembelajaran mesin yang tak terbatas. Artinya, kami dapat mengekstrak beberapa batasan ketidakpastian dan informasi statistik dari prediksi Anda. Hasilnya tidak hanya "10,23", tetapi lebih seperti "10,23 dengan kemungkinan kesalahan 0,50".

Saya harap saya membuat Anda bersemangat. Mari kita ke bab selanjutnya

2. Beberapa matematika

Saya tidak ingin artikel ini menjadi basa-basi, tetapi saya tidak ingin itu menyakitkan. Jika Anda mendapatkan ide tentang Bayesian Neural Network, atau jika Anda sudah mengetahui matematika yang ada di baliknya, silakan lewati bab ini. Jika Anda ingin memiliki referensi, yang baik adalah sebagai berikut. (Hands-on Bayesian Neural Networks — Tutorial untuk Pengguna Deep Learning)

Sekarang semua ini tampak keren dan keren, tetapi saya pikir jika Anda adalah pengguna pembelajaran mesin, Anda memiliki pemikiran ini:

"Bagaimana saya bisa mengoptimalkan makhluk aneh seperti itu?"

Jawaban singkatnya adalah, “Dengan memaksimalkan:

Tetapi saya tidak berpikir bahwa ini cukup jelas.

Dalam hal ini, prinsip optimasi adalah mencari estimasi terbaik dari distribusi p(w|D). Kami akan menyebut distribusi ini q, dan kami menginginkan metrik jarak antara dua fungsi distribusi.

Metrik yang akan kita gunakan disebut divergensi Kullback–Leibler

Beberapa fakta menarik tentangnya:

Ini adalah 0 untuk dua distribusi yang sama

Tak terhingga jika penyebut kedua distribusi cenderung nol sedangkan pembilangnya tetap bukan nol

Itu tidak simetris.

Sekarang fungsi kerugian yang Anda lihat di atas adalah kuantitas pengganti untuk divergensi Kullback-Leibler, dan ini disebut bukti batas bawah (ELBO).

Distribusi bobot q dianggap sebagai distribusi normal dengan rata-rata mu dan varians sigma2:

Jadi pengoptimalannya adalah tentang menentukan nilai mu dan sigma terbaik untuk distribusi itu.

Dalam implementasi praktis PyTorch, MSE antara rata-rata distribusi dan target juga ditambahkan ke L (mu, sigma) kita.

3. Implementasi Pyt(orch)hon

Implementasi jaringan saraf Bayesian di Python menggunakan PyTorch sangat mudah berkat perpustakaan yang disebut torchbnn.

Menginstalnya sangat mudah dengan:

pip install torchbnn

Dan seperti yang akan kita lihat, kita akan membangun sesuatu yang sangat mirip dengan jaringan neural Tor standar:

model = nn.Sequential(
    bnn.BayesLinear(prior_mu=0, prior_sigma=0.1, in_features=1, out_features=1000),
    nn.ReLU(),
    bnn.BayesLinear(prior_mu=0, prior_sigma=0.1, in_features=1000, out_features=1),
)

Sebenarnya, ada perpustakaan untuk mengonversi model obor Anda menjadi pengganti Bayesian:

transform_model(model, nn.Conv2d, bnn.BayesConv2d, 
                args={"prior_mu":0, "prior_sigma":0.1, "in_channels" : ".in_channels",
                      "out_channels" : ".out_channels", "kernel_size" : ".kernel_size",
                      "stride" : ".stride", "padding" : ".padding", "bias":".bias"
                     }, 
                attrs={"weight_mu" : ".weight"})

Tapi mari kita lakukan contoh terperinci dan langsung:

4. Tugas regresi langsung

Hal pertama yang harus dilakukan adalah mengimpor beberapa pustaka:

import numpy as np
from sklearn import datasets
import torch
import torch.nn as nn
import torch.optim as optim
import torchbnn as bnn
import matplotlib.pyplot as plt

Setelah itu, kita akan membuat dataset bidimensi yang sangat sederhana:

x = torch.linspace(-2, 2, 500)
y = x.pow(5) -10* x.pow(1) + 2*torch.rand(x.size())
x = torch.unsqueeze(x, dim=1)
y = torch.unsqueeze(y, dim=1)

plt.scatter(x.data.numpy(), y.data.numpy())
plt.show()

Jadi, dengan masukan 1D kita x (berkisar dari -2 sampai 2), kita ingin mencari y kita.

def clean_target(x):
    return x.pow(5) -10* x.pow(1)+1
def target(x):
    return x.pow(5) -10* x.pow(1) + 2*torch.rand(x.size())

Clean_target adalah generator kebenaran dasar kami, dan target adalah pembuat data berisik kami.

Sekarang kita akan mendefinisikan jaringan neural feed-forward Bayesian kita:


model = nn.Sequential(
    bnn.BayesLinear(prior_mu=0, prior_sigma=0.1, in_features=1, out_features=1000),
    nn.ReLU(),
    bnn.BayesLinear(prior_mu=0, prior_sigma=0.1, in_features=1000, out_features=1),
)

Seperti yang bisa kita lihat, ini adalah jaringan saraf feed-forward dua lapis dengan lapisan Bayesian. Ini akan memungkinkan kita untuk memiliki output probabilistik.

Sekarang kita akan menentukan kerugian MSE kita dan divergensi Kullback-Leibler yang tersisa:

mse_loss = nn.MSELoss()
kl_loss = bnn.BKLLoss(reduction='mean', last_layer_only=False)
kl_weight = 0.01

optimizer = optim.Adam(model.parameters(), lr=0.01)

Kedua kerugian tersebut akan digunakan dalam langkah pengoptimalan kami:

for step in range(2000):
    pre = model(x)
    mse = mse_loss(pre, y)
    kl = kl_loss(model)
    cost = mse + kl_weight*kl
    
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()
    
print('- MSE : %2.2f, KL : %2.2f' % (mse.item(), kl.item()))

2000 zaman telah digunakan.

Mari kita tentukan set pengujian kita:

x_test = torch.linspace(-2, 2, 300)
y_test = target(x_test)

x_test = torch.unsqueeze(x_test, dim=1)
y_test = torch.unsqueeze(y_test, dim=1)

Sekarang, hasil yang keluar dari kelas model adalah probabilistik. Ini berarti bahwa jika kita menjalankan model kita 10.000 kali, kita akan mendapatkan 10.000 nilai yang sedikit berbeda. Untuk setiap titik data dari -2 ke 2, kami akan mendapatkan rata -rata dan standar deviasi, dan kami akan merencanakan interval kepercayaan diri kami.

plt.figure(figsize=(10,8))
plt.plot(x_test.data.numpy(),mean_values,color='navy',lw=3,label='Predicted Mean Model')
plt.fill_between(x_test.data.numpy().T[0],mean_values-3.0*std_values,mean_values+3.0*std_values,alpha=0.2,color='navy',label='99.7% confidence interval')
#plt.plot(x_test.data.numpy(),mean_values,color='darkorange')
plt.plot(x_test.data.numpy(),y_test.data.numpy(),'.',color='darkorange',markersize=4,label='Test set')
plt.plot(x_test.data.numpy(),clean_target(x_test).data.numpy(),color='green',markersize=4,label='Target function')
plt.legend()
plt.xlabel('x')
plt.ylabel('y')

5. Membungkusnya

Dalam artikel ini, kami melihat cara membangun model pembelajaran mesin yang menggabungkan kekuatan jaringan saraf dan masih mempertahankan pendekatan probabilistik untuk prediksi kami.

Untuk melakukan itu, kita dapat membangun apa yang disebut Bayesian Neural Network.Idenya bukan untuk mengoptimalkan hilangnya jaringan saraf tetapi hilangnya jaringan saraf yang tak terbatas. Dengan kata lain, kami mengoptimalkan distribusi probabilitas parameter model kami yang diberikan dataset.

Kami melakukan itu menggunakan fungsi kerugian yang menggabungkan metrik yang dikenal sebagai Divergence Kullback-Leibler. Ini digunakan untuk menghitung jarak antara dua distribusi.

Setelah mengoptimalkan fungsi kehilangan kami, kami dapat menggunakan model yang probabilistik. Ini berarti bahwa jika kita mengulangi model ini dua kali kita mendapatkan dua hasil yang berbeda, dan jika kita mengulanginya 10k kali kita dapat mengekstraksi distribusi statistik yang kuat dari hasil kita.

Kami menerapkan ini menggunakan torch dan perpustakaan bernama Torchbnn. Kami membangun tugas regresi sederhana kami dan menyelesaikannya menggunakan jaringan saraf forward forward dua lapisan.